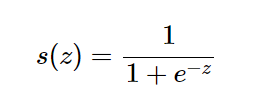티스토리 뷰
Logistic Regression(로지스틱 회귀)
참과 거짓을 예측하기 위한 알고리즘이다.
데이터에 선을 긋는 선형회귀와는 다르게 아래와 같이 0과 1에 닿는 S모양의 커브를 가지고 있다.

이 알고리즘은 머신러닝 지도학습에 사용된다.
Regression 이라는 이름을 보아 Regression(회귀) 문제 에 쓰일 것 같지않은가?
땡! 의외로 이 알고리즘은 지도학습의 이진분류에 쓰이며 Classification(분류) 알고리즘으로 구분된다!
S모양의 정 가운데(0.5)보다 위에 있는 것들은 참으로 분류하고 아래에 있는 것들은 거짓으로 분류하는 것이다. 선형구분이 가능할 때 퍼포먼스가 좋다.
Logistic Regression이 나타나는 과정
Logistic Regression은 결과값을 최대한 0과 1에 가깝게 만들어서 이것이 참인지 거짓인지를 구분하는 것 이라고 했다. 이것이 어떻게 가능할까?
Linear Regression 으로부터 시작되는 여정
먼저, Linear Regression을 보자. 입력값이 x로 주어지고 y가 결과값으로 나와야할 때 Linear Regression은 아래와 같은 방정식을 가진다. (w와 b는 머신러닝이 랜덤으로 정해주는 상수라고 생각하자.)
H(x) = Wx + b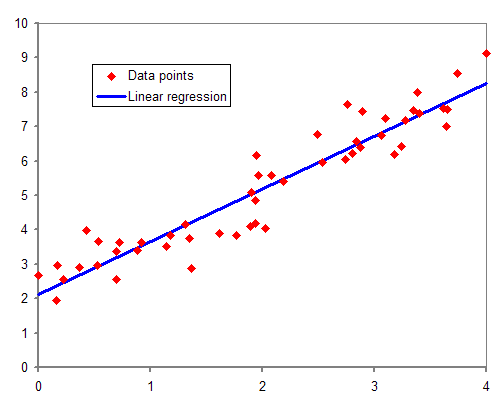
이 방정식의 x부분에 무엇을 넣어도 결과값이 y는 1보다 커지게되어있다. 심지어 마이너스가 될 수도 있다! 0과 1 사이의 값으로 구분하고 싶은데 영 쉽지않을 것 같다. 그래프를 보더라도 0과 1은 커녕 좌표평면을 아름답게 긋고만 있다.
0과 1에 가깝게! Sigmoid Function(시그모이드 함수)라는 Activation Function(활성화 함수)
Logistic Regression 에 나오는 함수라서 Logistic Function(로지스틱 함수) 라고도 하는 Sigmoid function 는 원하는 값을 도출하기 위해 사용되는 Activation Function(활성화 함수) 의 한 종류이다.
앞에서 봤듯이 단순히 Wx + b 라는 식으로 예측값을 0과 1 사이의 값으로 만든다는 것은 힘들기 때문에 Activation 함수인 Sigmoid 함수를 사용하여 예측값을 0과 1 사이의 값으로 만들어준다. 그렇게 하면 우리가 잘 아는 Logistic Regression 그래프가 만들어지고 기계는 이것을 가지고 분류를 하게된다.
Sigmoid 함수의 식
# 머신러닝에선 공간과 벡터를 다루기 때문에 이에 최적화되어있는 numpy 라이브러리를 사용한다.
# (실수를 다루는 math 라이브러리는 사용하지않는다)
import numpy as np
def sigmoid(z):
s = 1 / (1 + np.exp(-z))
return sLogistic Regression의 Cost Function(비용함수)
자, 이제 예측값을 알게되었으니 Cost Function(비용함수) 을 이용하여 데이터와 예측값의 오차를 구하고 그 오차를 최소화 할수있는 가중치와 편향값을 찾을 것이다.Linear Regression 의 경우에는 선형회귀의 비용함수식을 이용하여 볼록한 그래프가 나오게 되고, 그 그래프에서 Gradient Descent(경사하강법) 라는 방법으로 계속해서 미분해가며 기울기가 0인 부분, 즉, 오차값이 최소인 부분의 가중치와 편향값을 구한다.
설레는 마음으로 Linear Regression 이 사용했던 비용함수를 Logistic Regression 에게도 적용해본다.
※ Cost Function(비용함수)란? - 훈련세트들이 얼마나 잘 추측되었는지 측정해주는 함수로 오차를 표현해주는 미분 가능한 함수이다.

앞서 시그모이드함수를 이용하여 그래프를 엄청나게 튜닝해두었더니 Linear Regression 에서는 예쁘게 잘 적용되었던 비용함수가 Logistic Regression에서는 못생기고 울퉁불퉁한 놈이 되어버렸다!! Gradient Descent(경사하강법) 을 사용하여 기울기가 0인 부분을 찾아야하는데 기울기가 0인 부분(최소오차)이 여러개가 생겨버리는 것이다. 국민선형회귀의 국민비용함수식으로 쉽게쉽게 가려고했는데 적용이 되질않는다. 어쩔 수 없다. Gradient Descent(경사하강법)를 사용하기 위해선, 기울기가 0인 부분을 잘 찾을 수 있는 새로운 비용함수가 필요하다.
그래서 아래와 같은 손실 함수를 이용한 비용함수를 사용한다.

Logistic Regression의 손실함수
(단일 훈련 셋에서 손실이 얼마나 발생했는지 측정해주는 함수)

Logistic Regression의 비용함수( Binary Cross Entropy 함수라고도 한다.)
(모든 입력에 대해 계산한 손실 함수의 평균 값)
import numpy as np
def cost():
A = sigmoid(np.dot(w.T, X) + b)
cost = -1/m * np.sum(Y * np.log(A) + (1-Y) * np.log(1-A))
return cost위 비용함수식을 이용하면 울퉁불퉁하지않고 볼록한 형태의 비용함수 그래프가 나타나게 되고, 이를 이용해서 기울기가 0인 부분(비용최소값)을 찾아주게되고, 이 것을 이용하여 최적화를 할 수 있게된다.
참고
Coursera - Logistic Regression
'ML' 카테고리의 다른 글
| 2. 미니배치 경사하강법 (Mini-batch Gradient Descent) (0) | 2023.07.24 |
|---|---|
| 1. 경사하강법과 역전파 정리 (0) | 2023.07.24 |
| 불균형 데이터 다루기 - Resampling (over-sampling, under-sampling) (0) | 2021.09.11 |
| 로지스틱 회귀와 신경망의 차이 (0) | 2021.08.15 |
| 역전파와 경사하강법의 차이점 (0) | 2021.08.14 |